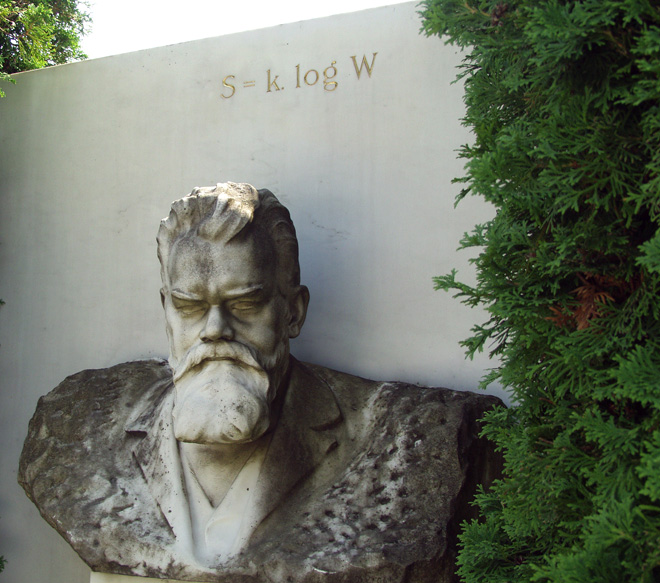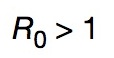Wired Science 挑选出了 9 个真正的 Geek 应该知道（至少要假装知道）的方程式。这些方程式有的代表了宇宙，有的代表了生命本质。世界的复杂与不确定性浓缩为一幅幅有序的图片，配上几个简单的符号就足以捕捉宇宙的奥秘（嗯，实际上可真是未必，不过至少目前来看还是可以这么 YY 一下的。）。
1. 美丽的等式：欧拉公式¶
也称为欧拉关系，或复数欧拉方程，这个数学关系简直有跨极客范围的荣誉。
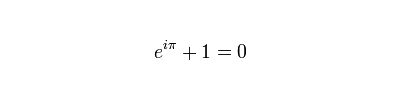瑞士数学家 Leonhard Euler 首先提出这一公式，将几何、代数以及数学中 5 个最基本的符号联系到了一起。这 5 个基本符号 0, 1, i, pi 和 e 是科学工作中的基本工具。
理论物理学家 Richard Feynman （费曼）是他的超级粉丝，并称赞该方程是宝贵且卓越的公式。如今，人们称之为最优美的等式。
Image: Cory Doctorow/Wikipedia
2. 数字化宇宙：弗里德曼方程¶
由爱因斯坦广义相对论导出的 2 个 Friedmann 方程描述了整个宇宙的生命轨迹：诞生于火热的大爆炸（Big Bang），终结于冰冷的加速膨胀。
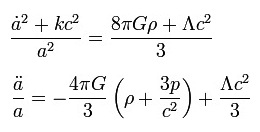这一组方程包含一个诡异的东西，被称为宇宙常数（没有底的三角形），最初由爱因斯坦引入，用于抵消重力以保持宇宙永恒不变。当天文学家观察到宇宙实际上是在膨胀的时候，爱因斯坦将其称为自己犯过的最大错误。近期的一些实验又给爱因斯坦平了反，因为实验显示存在一个巨大而神秘的力量在加速宇宙的膨胀。人们称之为暗能量。暗能量的发现被评为 2011 年度诺贝尔物理学奖，不过要弄明白它究竟是怎么回事儿还是让科学家们很费脑子。
Image: NASA / WMAP Science Team
3. 玻尔兹曼熵公式¶
自然热爱混乱，它将系统推向平衡，极客称之为 property entropy（我不是极客，搞不清楚这个是不是该译为属性熵，或者财产熵？）。
奥地利物理学家 Ludwig Boltzmann 奠定了熵的统计学基础。他的工作如此重要，因而在伟大的物理学家 Max Planck 的建议下，将他的版本的玻尔兹曼公式刻在了位于维也纳的玻尔兹曼的墓碑上（上图）。
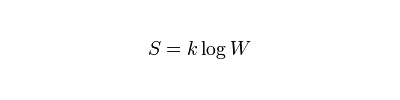玻尔兹曼熵公式描述了熵（S）和系统中巨量粒子的分布规律（k·logW）。公式的后一部分是很复杂的。k 是玻尔兹曼常数，W 是处于平衡状态的微观系统（）例如，封闭在瓶子中的气体）中的微观单元的数目（例如，气体中各个原子的动量和位置）。
注意：不要将该式与另一个描述气体或流体传导能量规律的玻尔兹曼（热传导）方程混淆了。
Image: Tom Schneider（链接已失效 http://www-lmmb.ncifcrf.gov/~toms/icons/boltzmann/boltzmann-tomb-8.html）/NCI-Frederick
4. 电磁场方程：麦克斯韦方程组¶
没有这四个方程，就不会存在潜伏于互联网的 lolcat。该方程组由 James Clerk Maxwell 于 1861 年联立起来，可以描述所有已知的电场、磁场以及它们之间相互作用的规律。它们揭示出运动的电荷会产生磁场，而变化的磁场也可以产生电场。
麦克斯韦方程组
第二个等式，磁场的高斯定理，还揭示了电场与磁场之间的微妙差别。电荷可以（正负电荷）独立存在，象电池的正负极；而磁却总是成对出现，你无法将磁铁的北极和南极分开。一些现代物理模型断定宇宙中可能存在少量没有北极或者没有南极的磁体（磁单极子）。有些科学家正在忙于通过实验证明它们的存在。
Image: The Z machine, largest x-ray generator in the world. Courtesy Sandia National Laboratories
5. 确定的不确定性：薛定谔方程¶
薛定谔方程
Erwin Schrödinger 著名方程统治着宇宙中最小的对象。它揭示出在力的作用下亚原子粒子随时间改变的规律。任意微小的原子或分子的波函数，描述了该粒子在何时何地出现的概率，由希腊字母 psi 表示。
不幸的是，在量子力学发展的早期，物理学家不知道该如何诠释薛定谔方程。一些赞成该思想的人认为波函数只是一个有用的计算工具，并不对应于任何现实的东西。另一些人认为它给我们能够认知的宇宙范围做出了限制，因为我们只在测量出来的时候才知道一个粒子处于什么状态。
不过薛定谔自己坚持认为，波函数描述的是真实的物理对象。他同意测量导致微粒坍塌的解释，也提出了著名的“薛定谔的猫”（一个假想的实验）来说明这种解释的不足之处。
Image: The ghostly tracks of subatomic particles in a hydrogen bubble chamber. Courtesy of CERN
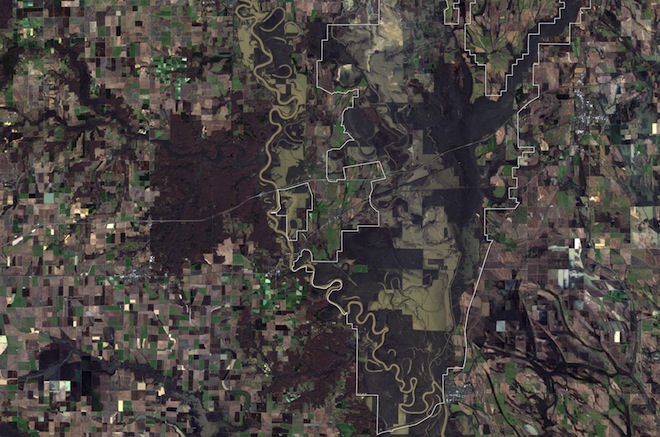
6. 所有生命都是岛：岛屿生物地理学理论¶
岛屿生物地理学公式
虽然物理学家能够用几行（表达式）来描述宇宙的膨胀，可地球上生命的基本属性却非常难以量化。20 世纪后半叶，生物学家渐渐形成了岛屿生物学理论，可用于描述岛屿上动物数量的动态变化。等式左边是某个给定岛屿能够支撑的物种数目；等式右边则是动物丰度，可用区域（面积）和迁入/迁出速率。该理论已经由海洋岛屿扩展到包括多种生态类型的区域，特别是那些与人类活动隔离的区域。除极地之外，几乎所有的自然环境现在都包含在人类定义的岛屿概念范围之内 —— 其中最大的岛屿自然就是地球。
Image: The Cache River wildlife preserve in Arksansas, an isolated patch of bottomwoods swamp where the extinct Ivory-Billed Woodpecker was reportedly seen. (NASA)
7. 进化理论：生物演化方程¶
进化方程
从最基本的层面来讲，生命就是自我复制 —— 但又是怎么开始的呢？这是个先有鸡还是先有蛋的问题，也是科学家研究的前生命理论试图回答的问题。方程的左边，是由哈佛大学数学生物学家 Martin Nowak提出的一个符号，代表所有可能的分子链；方程的右边是化学反应速率，由较短分子链向较长分子链变化的趋势，选定的压强和满意度水平。 就像 Nowak 展示的，生命诞生所需要的所有条件依赖于选择和变异的（相互作用）力。只要满足这些条件，在重力的作用下（因为重力是不可避免的），自我复制就会随之出现。
Image: Sunrise over California’s Mono Lake, a hot, oxygen-deprived, arsenic-rich lake that scientists think mimics conditions on early Earth. (NASA)
8. 爆发前沿：R0¶
R-nought
由令人恐怖的大传染引起大众注意的 R0，读作 R-nought，是一个非常简单的数字，它表示：某个体感染了某种病毒后继续传染给其他人的平均数目。如果该数值小于 1，该疾病就会自己消失；如果大于 1，它就会传播开来。在一个从墨西哥爆发的流感病毒能够在数月内感染世界上数百万人口的世界，这个等式的含义就像它的表达符号那么直接。
Image: Subway riders in Mexico City during the 2009 swine flu outbreak. (Eneas de Troya/Flickr)
9. 美丽的数学极限¶
并不是所有的东西都可以量化，特别是那些与人类心理和精神相关的事物。数十年来，心理学家和生物学家都尝试用公式（的形式）来表达人体的美；但即便是考察了成百上千个个体的偏好之后能够得到一些趋势，也还是无法预测某一个体以什么样的标准来看待美。
一个以色列计算机科学家未公开发表的公式（如右所示）尝试设计一个能够量化人脸吸引力的程序。”Y” 是美丽的经验分值；等式右边是表示脸上的各种不同形状与基准脸型相比较得到的各种测量数据。该程序代码写得非常棒，但是运行结果却并不太好。
Image: Pierre Tourigny/Flickr
版权声明：
该文主要编译自 Wired.com 上的相关文章，并且未曾获取其许可。如需转载，请自行联系 Wired.com 网站。
我大胆编译转发，是因为看到该文配图也有取自遵循 Attribution-ShareAlike 2.0 Generic (CC BY-SA 2.0) 网络分享协议的网站的。
原文链接：
9 Equations True Geeks Should (at Least Pretend to) Know
本文发表于水景一页。永久链接：<https://cnzhx.net/blog/9-equations-true-geeks-should-know/>。转载请保留此信息及相应链接。